Regular Expressions and Finite Automata

A couple months ago, I built rexen, a tool that compiles and evaluates regular expressions (regexes) using Non-deterministic Finite Automaton (NFA). Regexes are pretty ubiquitous in computer programming and this was my attempt at understanding how they work.

A regular expression (regex) is a sequence of characters/symbols that abstractly represent or define a set of strings (also known as a regular language). For example, the regex a*b defines the set of strings { b, ab, aab, aaab, aaaab, ... } ie. zero or more a's followed by a b.

The question is

Given a string, how can we determine if it is a member of the set defined by a regex? In other words, how can we check that a string conforms to the pattern specified by a regex?

If this were a plain string comparison, it’d be as straightforward as checking that the two strings are of the same length and that they have the same characters at each index ie. the string bob matches the string bob because it fulfills the requirements above. But with regexes, we’re not dealing with simple 1:1 mappings as a single regex can match multiple (and possibly infinite) number of strings. So, we need a different strategy.

The idea is to represent the regex as a bunch of (linked) steps or states and try to evaluate the input string by simulating it through these states, if we reach a desired end state then we can be sure that the string is indeed a member of the set defined by that regex.

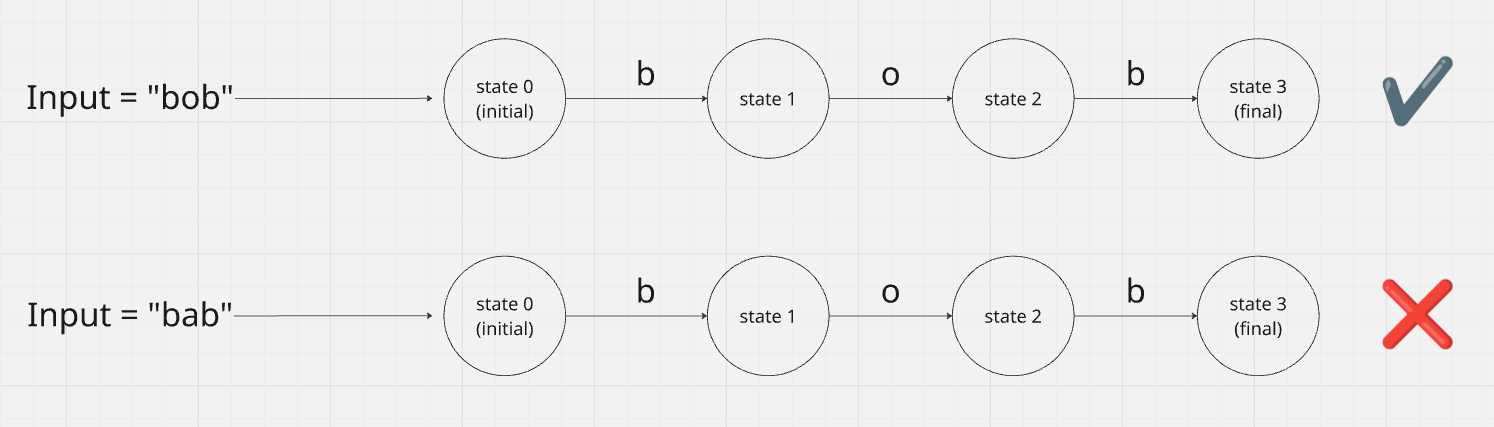
In the contrived example below, the string bob satisfies the requirement to incrementally move from the initial state up until the end state, so we can conclude that it matches the pattern specified by the regex. In contrast, the string bab fails to meet the requirement to move from state 1 to 2 and since there is no other logical way to get to the end state, we can conclude that it fails to match the regex pattern. This idea is formally referred to as a finite automata or finite state machine.

A Finite Automaton (FA) is a mathematical model that can be in one of a limited number of states and can transition between them in reaction to an input/event. It consists of a finite set of states, an initial state, a transition function that defines the rules to go from one state to another and (optionally) a set of end states. For example, a light bulb can be in only one of two states at a time (off or on) and can transition between these states based on an external signal from a switch.

There a two types of FAs: Deterministic Finite Automaton (DFA) and Non-deterministic Automaton (NFA). The major difference between the both of them is that in a DFA, every state has exactly one transition for each possible input while in an NFA, an input can lead to one, more than one, or no transition for a given state. Technically, all NFAs can be represented as (possibly more complex) DFAs and there are a number of algorithms to convert an NFA to its corresponding DFA.

Converting Regexes to NFA

To convert a regular expression to NFA we go through the following steps:

1. Split the regex string into distinct tokens and establish operator precedence. Operator precedence determines the order in which operations are performed in a given expression - operators with a higher precedence are applied before ones with lower precedence. Here is a list of operators in rexen in order of descending precedence.

• Kleene Star * (zero or more of the preceding character or group of characters).
• Concatenation (character or group of characters before the operator followed by the character or group of characters after the operator).
• Union + (one of the characters or group of characters before or after the operator).

Concatenation in rexen and in most regex engines is implicit, that means, there is no symbol that represents it. But for the sake of simplicity, we explicitly inject an operator while tokenizing. ie the expression ab becomes a(Concat)b.

Operators like + (one or more of the preceding character or group of characters) and ? (zero or one of the preceding character or group of characters) are variations of the Kleene star operator * and as such have equal precedence.

2. Convert from infix to postfix (reverse polish) notation using the Shunting-Yard Algorithm (SYA). Postfix notation is a mathematical notation in which operators follow their operands whereas in infix notation, operators are placed between their operands (e.g., a + b in infix becomes a b + in postfix).
   The main advantage of using postfix notation is that it resolves operator precedence, removing the need for using parentheses. It also allows for an expression to be evaluated from left to right which is suitable for stack based computation. SYA works by reading the input one character at a time from left to right and performing one of the following:

• If it is a literal ie. not an operator or a parentheses, append it to the output buffer.
• If it is a left parentheses (, push it onto the stack.
• If it is an operator and there is a left parentheses ( on top of the stack or the stack is empty, push the operator onto the stack.
• If it is a right parentheses ) pop all operators on the stack and append it to the output buffer. Do this until a ( is encountered or the stack is empty (an empty stack indicates an error as there is no corresponding opening parentheses).
• If it is an operator and the operator on top of the stack has a higher or equal precedence, pop that operator and append it to the output buffer. Do this until the operator on top of stack has a lower precedence than the current operator from the input or the stack is empty, then append the operator to the stack.
  Here is an implementation in pseudocode:

input := "a(a+b)"
stack := []
output := []

for char in input:
    match char:
        case LParen: 
            stack.push(char)
        case RParen:
            loop:
                if stack is empty:
                    return error
                top := stack.pop()
                if top == LParen:
                    break
                output.append(top)
        case Operator:
            while stack is not empty:
                top := stack.peek()
                if top == LParen:
                    break
                if top has a higher or equal precedence to char:
                if precedence(top) >= precedence(char):
                    stack.pop()
                    output.append(top)
                else
                    break
            stack.push(char)
        case AnythingElse:
            output.append(char)

# after consuming the input
while stack is not empty:
    top := stack.pop()
    if top == LParen:
        return error
    output.append(top)

# output now becomes aab+.

3. The final step in the conversion process is to utilize the Thompson’s construction algorithm. The algorithm works by breaking down a regular expression into its component parts and building a simple NFA for each part. These smaller NFAs are then combined using a set of rules:

• For empty expressions "" return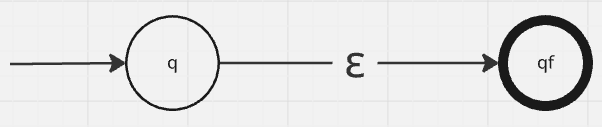
• For single character expressions ie a return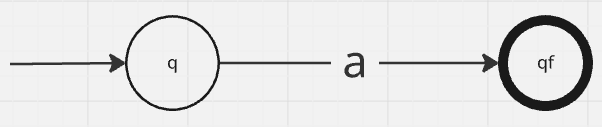
• For union expressions ie a|b (a or b) we first create different nfas for a and b and then join them together by creating a new initial state (q) with an epsilon transition from q to the initial states of the nfas for a and b and an epsilon transition from final states of a and b to a new final state qf.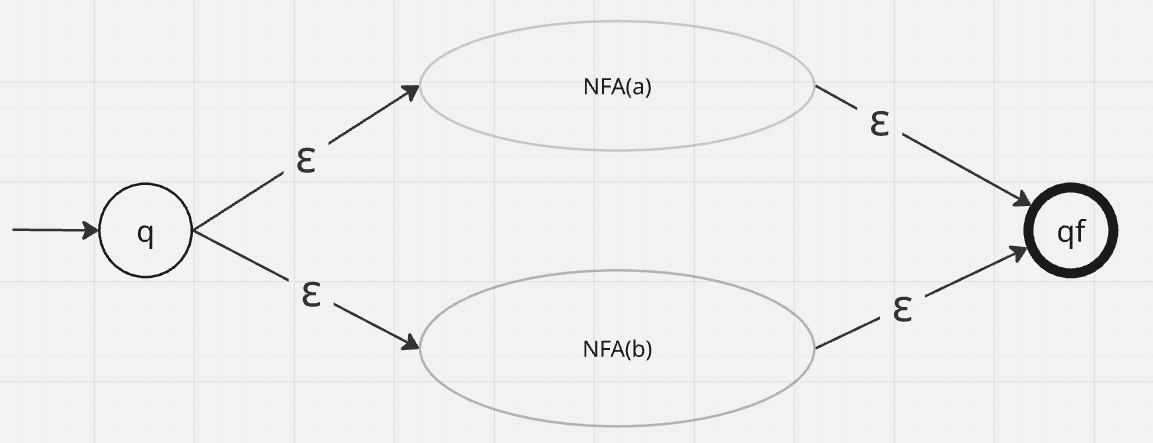
• For concatenation ab (a followed by b) we create the individual nfas for a and b and connect them together by creating an epsilon transition from the end state(s) of NFA(a) to the initial state of NFA(b).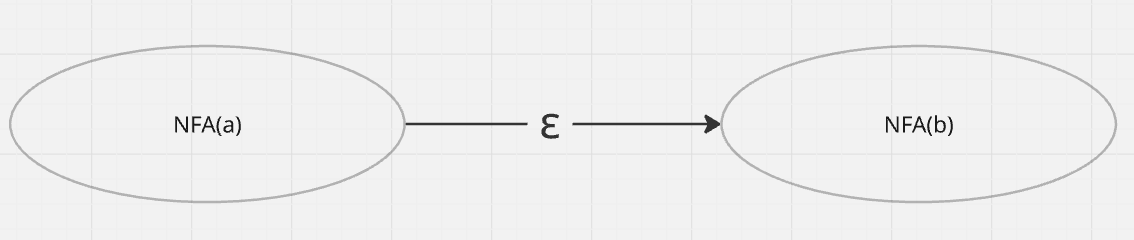
• For closure a* (zero or more occurrences of a) we create two new states q and f then we create a transition from q to f, from q to the initial state of NFA(a), from the end state of NFA(a) to f and then from the end state of NFA(a) to its initial state.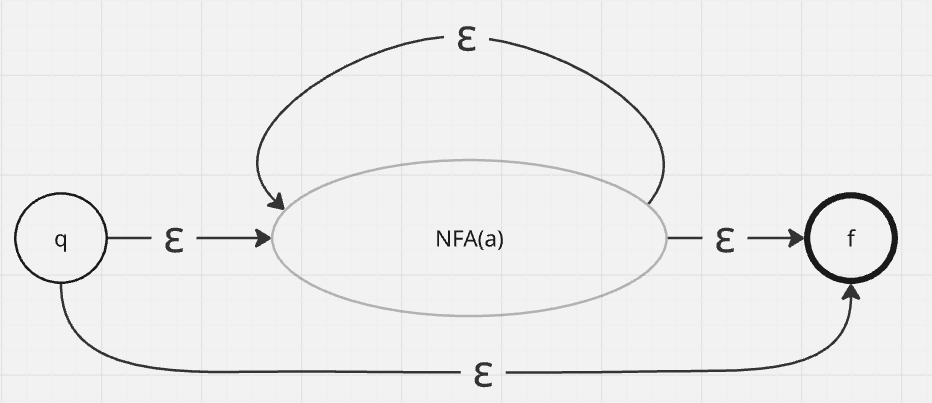

The names we call the states are really not important. We just have to make sure that the names of each states are unique to avoid collisions when trying to transition between states. Also, if you ever need to visualize the nfa, it’s easier to differentiate between states if they have different labels.

input := "aab+" # expression in postfix form.
for each token in input:
    if token is a character:
        nfa := create basic NFA for character
        stack.push(nfa)

    else if token is concatenation '.':
        nfa2 := stack.pop()
        nfa1 := stack.pop()
        newNFA := concatenate(nfa1, nfa2)
        stack.push(newNFA)

    else if token is alternation '|':
        nfa2 := stack.pop()
        nfa1 := stack.pop()
        newNFA := alternate(nfa1, nfa2)
        stack.push(newNFA)

    else if token is Kleene star '*':
        nfa := stack.pop()
        newNFA := kleeneStar(nfa)
        stack.push(newNFA)

return stack.pop()

Function create basic NFA for character c:
    start ← new state
    end ← new state
    add transition (start → c → end)
    return NFA(start, end)

Function concatenate(nfa1, nfa2):
    add ε-transition from nfa1.accept to nfa2.start
    return NFA(nfa1.start, nfa2.accept)

Function alternate(nfa1, nfa2):
    start ← new state
    accept ← new state
    add ε-transitions: (start → nfa1.start), (start → nfa2.start)
    add ε-transitions: (nfa1.accept → accept), (nfa2.accept → accept)
    return NFA(start, accept)

Function kleeneStar(nfa):
    start ← new state
    accept ← new state
    add ε-transitions: (start → nfa.start), (nfa.accept → accept)
    add ε-transitions: (start → accept), (nfa.accept → nfa.start)
    return NFA(start, accept)

Evaluating an Input String by Simulating an NFA

To determine whether an input string matches the pattern defined by a regular expression and its corresponding NFA, it’s important to specify the type of match desired: whether prefix, suffix, or full-string. Rexen performs a full-string evaluation, meaning it attempts to match the entire input string against the NFA, rather than just a portion of it. During this process, it simulates all possible paths the NFA can take by checking each transition against the current character in the input stream. A match is successful if there exists at least one path from the initial state to a final state and the input string has been fully consumed by the end of the traversal.